Единицы измерения в начальной школе и 5 классе

На уроках математики в начальной школе дети учатся измерять длину, ширину, высоту, расстояние, вес, объём, площадь фигуры и разбираются в единицах времени. Давайте посмотрим, какие есть единицы измерения для этих величин.

Переводим единицы измерения времени

Папа предупредил, что через час приедет бабушка. Мама сказала, что нужно поторопиться и выходить через 10 минут, чтобы успеть в кино. Брат вообще крикнул, что надо бежать, а то мультики уже через двадцать секунд. Почему в одном случае нужно бежать, в другом делать что-то просто побыстрее, а в третьем – можно спокойно готовиться к приходу бабушки?

Секунда – это единица измерения времени, которая очень мала и быстро пролетает. Достаточно произнести «раз и» – и секунда закончилась. Поэтому если осталось несколько секунд, всё нужно делать очень-очень быстро.

Следом за секундой идёт минута. Она уже подлиннее. Если минут мало, нужно действовать быстро, если много – можно замедлиться. В 1 минуте 60 секунд. Вспомним наш пример в начале статьи о том, что до дома идти 300 секунд. Это на самом деле не очень долго – всего 5 минут.

Самая длинная из этих единиц измерения – час. В часе 60 минут или 3600 секунд. Если есть час или несколько часов, можно спокойно заниматься делами – всё успеешь. Если не лениться. Чтобы было нагляднее, посмотрим в таблицу:

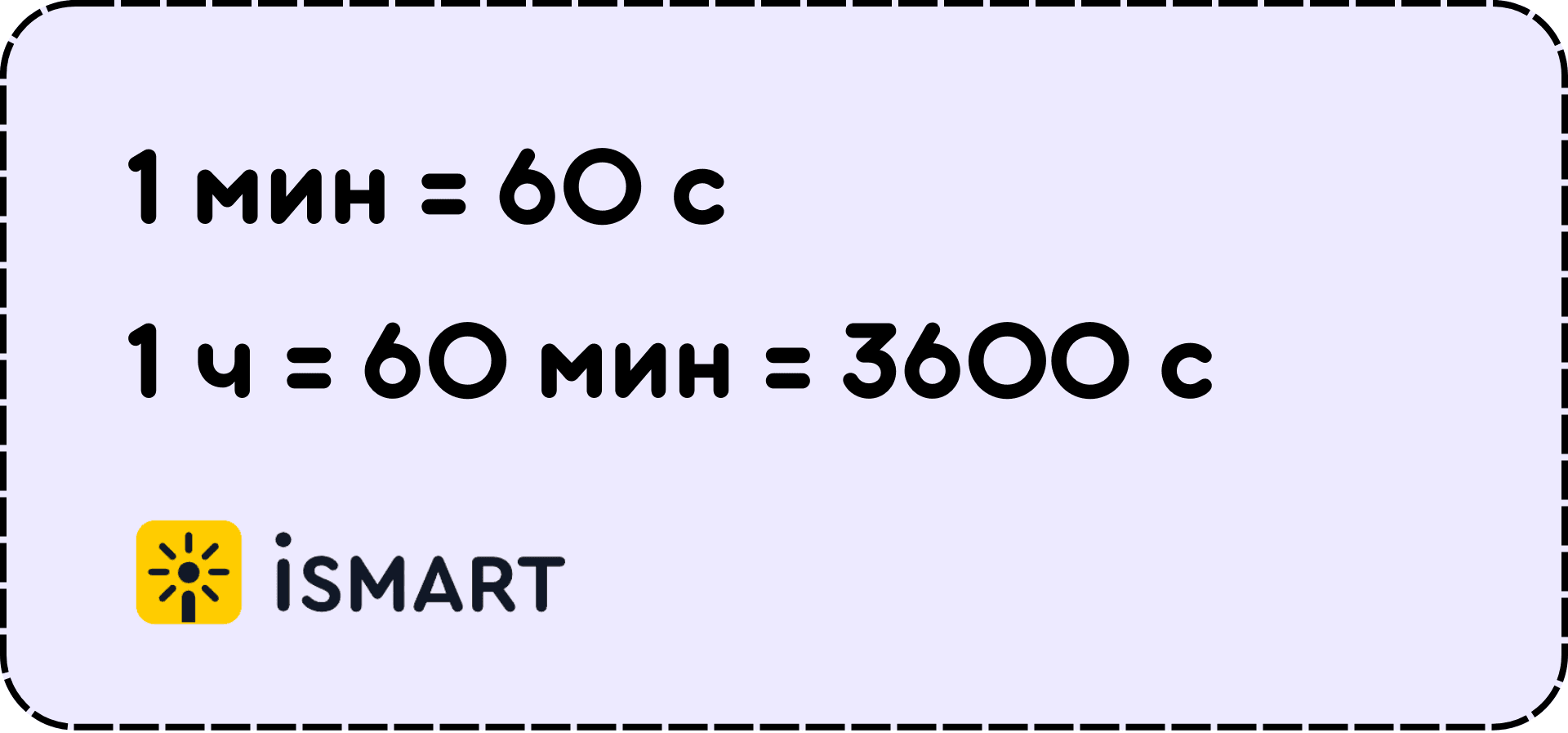
Теперь попробуем перевести секунды в минуты и обратно.

Задача №1

Решение: 1 минута = 60 секунд. Нужно понять, сколько раз по 60 секунд помещается в числе 120. Используем деление. 120:60=2 (мин).

Ответ: 2 минуты Крош потратил, чтоб допрыгать до дерева.

Подсказка! Чтобы было легче считать, убираем ноли в том и в другом числе (и в делимом, и в делителе). Всегда убираем равное количество нолей. 12:6=2.

Задача №2

Решение: Мы знаем, что 1 час = 60 минут. Значит, чтобы узнать, сколько минут в трёх часах, нужно 60 минут взять 3 раза. Используем умножение. 60x3=180 (мин).

Ответ: за 180 минут Гарри нашёл заклинание.

Подсказка! Сначала умножь 6 на 3, а потом подставь 0. Правило действует, только если числа оканчиваются на ноль.

Задача №3

Решение: Мы знаем, что 1 час = 60 минут.

Если мы ехали 2 часа, нужно 60 умножить на 2. Получаем 120 минут. Но мы ехали 2 часа и 40 минут. Поэтому к 120 минутам прибавляем 40 минут. (60 x 2) + 40=120+40=160 (мин)

Ответ: 160 минут мы ехали до дачи.

Граммы, килограммы, тонны

Грамм – самая малая единица веса, изучаемая в младших классах. Далее идет килограмм. Этими единицами измерения мы часто пользуемся в обычной жизни при походе в магазин. Но если нужно взвешивать тяжелые промышленные грузы, их измеряют в центнерах и тоннах.

Задача №1

Решение: Мы знаем, что 1 кг = 1000 г. Нужно понять, сколько раз по 1000 г помещается в числе 4000. Используем деление. 4000:1000=4 (кг)

Ответ: 4 килограмма весит арбуз.

Не забываем про подсказку и убираем ноли в том и в другом числе. Убираем всегда одинаковое количество нолей. 4:1=4.

Задача №2

Решение: Мы знаем, что 1 кг = 1000 г. Полкило – это половина килограмма. Когда ищем половину, всегда делим целое на две части. Значит, нужно наш килограмм, который равен 1000 г, поделить на две части. 1000:2=500 (г)

Ответ: полкило сыра – это 500 г, так что кусок сыра в 300 г мне не подойдёт.

Задача №3

Решение: Мы знаем, что 1 т = 1000 кг. Нужно понять, сколько раз по 1000 кг помещается в числе 26 000. Используем деление. 26 000:1000=26 (т).

Ответ: 26 тонн зерна вёз поезд.

Подсказка! Всегда в таких случаях убираем ноли в том и в другом числе. Здесь убираем по три ноля. 26:1=26.

Сантиметры в метры

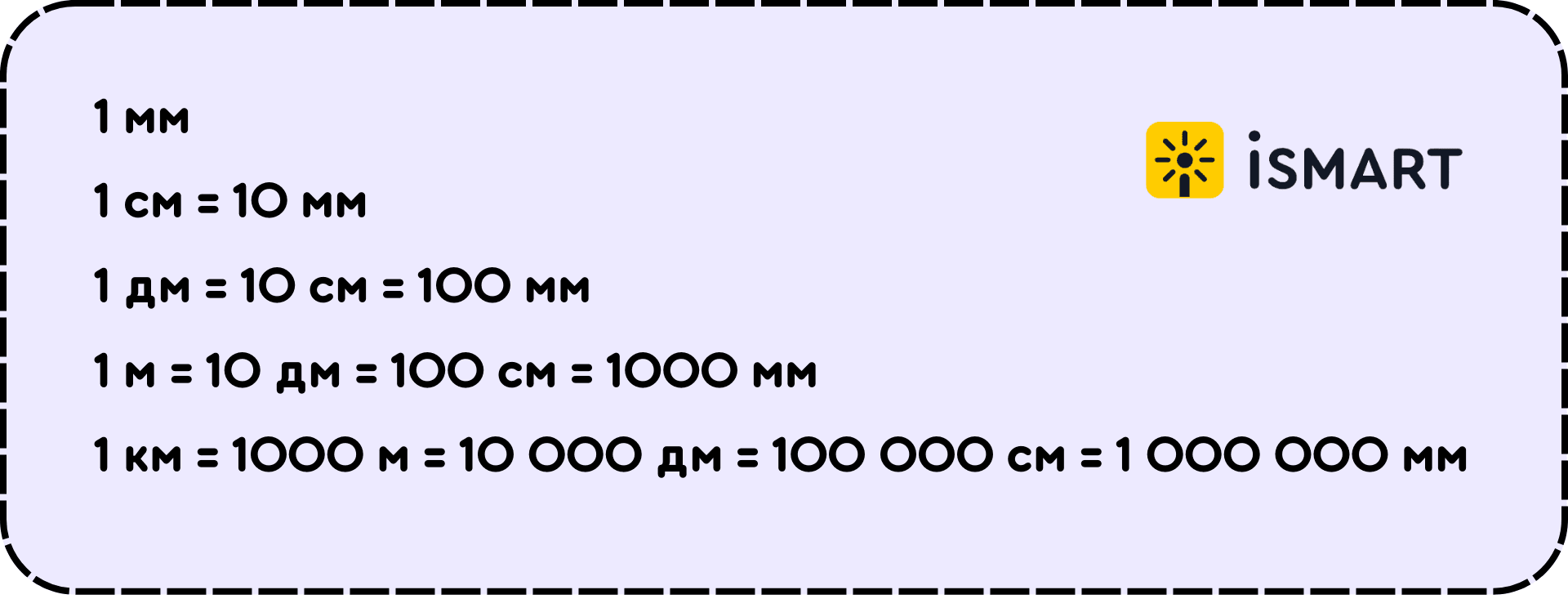
Длину, ширину и высоту в школе измеряют в миллиметрах, сантиметрах, дециметрах и метрах. Для измерения маленьких отрезков подойдёт линейка. Самое маленькое деление – 1 миллиметр. Каждая следующая единица измерения увеличивается в 10 раз.

1 см равен 10 мм, 1 дм – 10 см, 1 м – 10 дм.

Если измеряем длинные расстояния, то делаем это в километрах. В 1 километре 1000 метров.

Задача №1

Решение: Мы знаем, что 1 дм = 10 см. Значит 3 дециметра будет равняться 30 сантиметрам. Прибавляем к 30 сантиметрам ещё 5 см получаем длину нашего отрезка из задачи. (3 x 10) + 5= 30+5=35 (см).

Ответ: 35 сантиметров – длина отрезка.

Задача №2

Решение: Мы знаем, что 100 см = 1 м. Чтобы узнать, сколько метров в 1000 см нужно тысячу разделить на сто. 1000:100=10 (м)

Ответ: 10 м ленты попросила отрезать мама.

Подсказка! Можно решить проще. Мы знаем, что 100 см = 1 м. У нас не 100, а 1000 см. Если мы количество сантиметров увеличили в 10 раз, значит, и количество метров увеличилось в 10 раз. Значит, 1000 см = 10 м.

Есть ещё один способ облегчить расчёты при переводе таких единиц. Когда переводим из сантиметров в метры — убираем 2 ноля. 1ØØ см = 1 м 10ØØ см = 10 м

Переводим единицы измерения площади

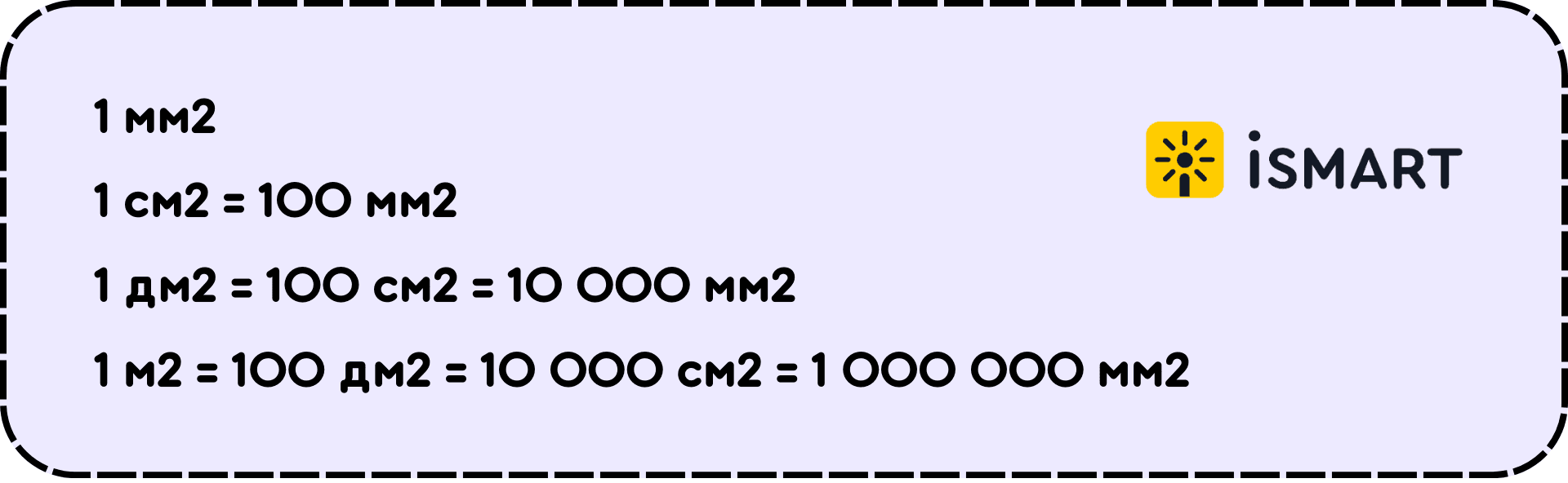
На уроках математики часто дают задачи найти площадь комнаты, участка, плоской геометрической фигуры. Площадь чего-то очень маленького измеряют в квадратных миллиметрах. Например, 25 мм² – площадь клеточки в тетради. После квадратного миллиметра идёт квадратный сантиметр и квадратный дециметр. В этих единицах чаще всего в школе измеряют геометрические фигуры. А если нужно измерить площадь квартиры или участка земли, её меряют в квадратных метрах.

Задача №1

Решение: Мы знаем, что 1 м² = 10 000 см². Значит, чтобы узнать, сколько квадратных сантиметров в 9 квадратных метрах, нужно 10 000 см² умножить на 9. 9 x 10 000=90 000 (см²).

Ответ: 90 000 см² – площадь батута в квадратных сантиметрах.

Подсказка! Сначала умножаем 9 на 1, а потом подставляем ноли из числа 10 000. Правило действует, только если числа оканчиваются на ноль.

Задача №2.

Решение: Мы знаем, что 10 000 см² = 1 м². Значит, нужно посчитать, сколько раз по 10 000 см² помещается в числе 20 000. Используем деление. 20 000: 10 000=2 (м²).

Ответ: 2 м² – площадь клумбы в метрах квадратных.

Помним про подсказку и убираем ноли в том и в другом числе. Убираем всегда одинаковое количество нолей. 2:1=2.

Как переводить единицы измерения объёма

Если в школе нам дают задачу измерить, сколько капель лекарства накапать в стакан, сколько воды нальётся в бассейн, попросят найти объём параллелепипеда, используем единицы измерения кубический миллиметр, сантиметр, дециметр и основную, которой чаще всего пользуются, единицу измерения – кубический метр.

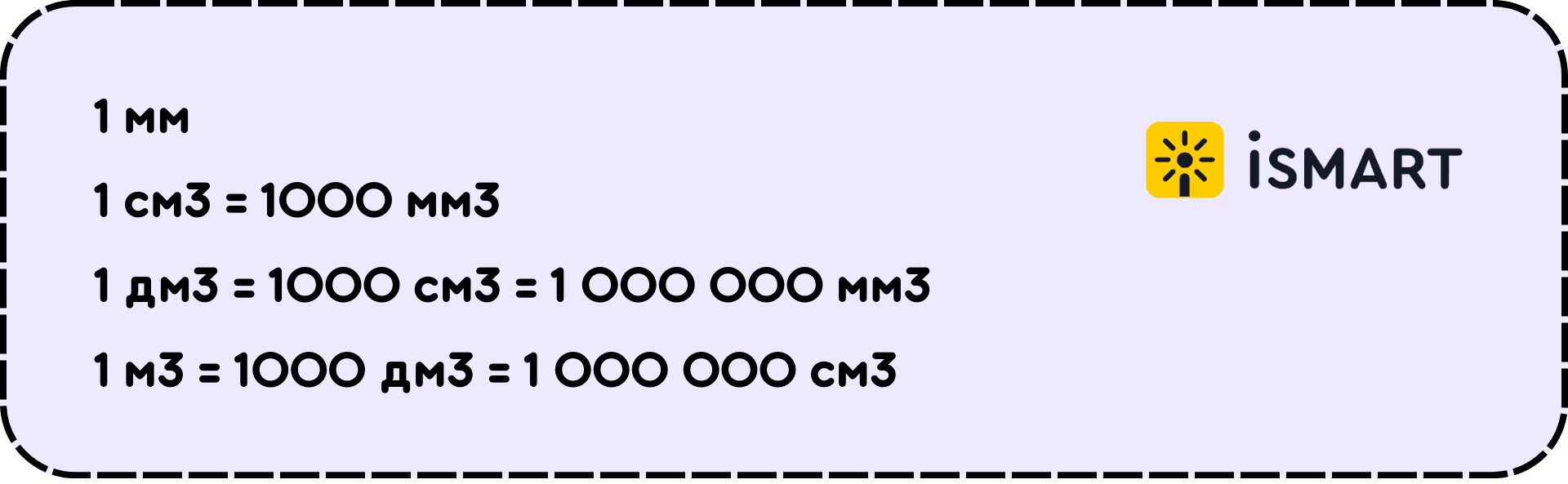
Пример №1.

Решение: Мы знаем, что 1 м³ = 1000 дм³. Значит, 3000 дм³ нужно разделить на 1000. 3000:1000=3 (м³).

Ответ: 3000 дм³=3 м³.

Пример №2.

Решение: Мы знаем, что 1 м³ = 1000 дм³. Значит, 1000 дм³ нужно умножить на 6. 1000 x 6=6000 (дм³).

Ответ: 6м³= 6000дм³.

Но у кубических сантиметра и дециметра есть и другие названия, которые мы все хорошо знаем и используем в обычной жизни. Про 1 см³ мы говорим миллилитр (мл), а про 1 дм³ – литр (л).

Измерять объём жидкостей в миллилитрах можно с помощью специальных стаканчиков с делениями, где каждое деление равно 1 мл (то есть 1 см³). Если измеряем что-то в литрах (то есть в дм³), можно взять тару, объём которой нам точно известен. Например, пакет молока. Если нужно измерять большие объёмы, пользуемся специальной формулой.

Пример №1

Решение: Мы знаем, что 1 л = 1 дм³. Значит, 1 дм³ нужно умножить на 4. 1 x 4=4 (дм³).

Ответ: 4л=4дм³.

Задача №1.

Решение: Мы знаем, что 1 л = 1000 мл. Значит, нужно узнать, сколько по 1000 мл помещается в числе 2000. Используем деление. 2000:1000=2 (л).

Ответ: 2 л молока нужно бабушке.

Не забываем про подсказку и убираем ноли (всегда равное количество) в том и в другом числе. 2:1=2.

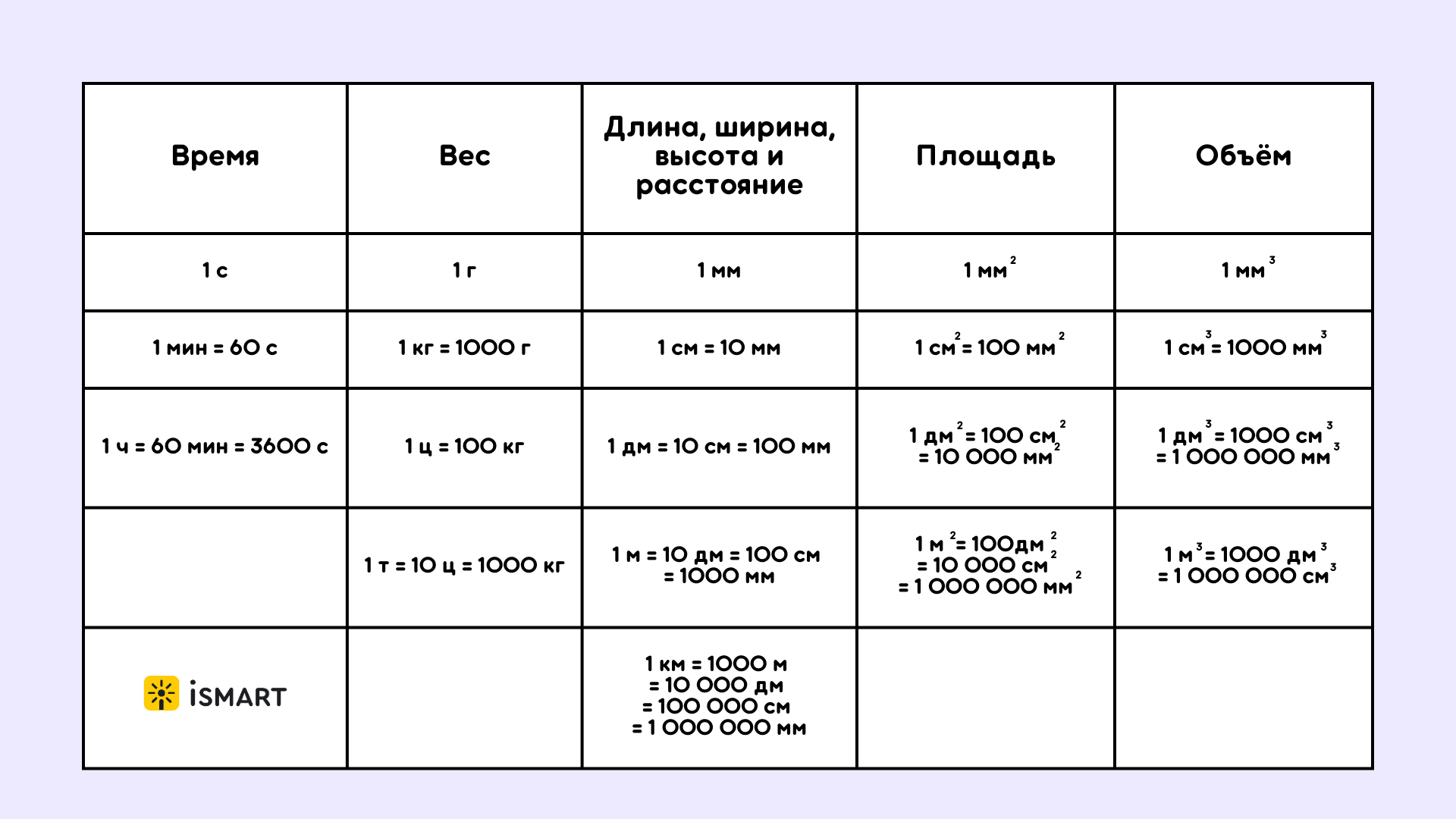
Сводная таблица перевода всех единиц измерения

Чтобы не искать каждый раз отдельную табличку, соединили все единицы измерения в одну сводную таблицу.

Как нужно рассуждать

Чтобы перевести одну единицу измерения в другую, есть ход рассуждения, который поможет всё сделать правильно.

•

Определите, с какими единицами измерения вы работаете. Можно переводить метры в сантиметры, но нельзя метры в литры (в метрах измеряем длину, а в литрах – объём).

•

Найдите соотношение между этими единицами. Например, 1 кг = 1000 г

•

Используйте соотношение, чтобы выполнить перевод. В 1 минуте 60 секунд, значит, в 2 минутах 120 секунд.

Онлайн-тренажёры по математике

Перевод единиц измерения – тема, которая требует внимательности, в ней легко запутаться. Чтобы у ребёнка не было страха при выполнении подобных задач, можно предложить попрактиковаться на онлайн-тренажёре по математике электронной образовательной платформы iSmart.

В зависимости от единицы измерения, задания относятся к 4 или 5 классу. Опыт родителей, которые уже воспользовались iSmart, показывает, что дети охотно занимаются каждый день или регулярно.

Система предлагает задания, исходя из текущего уровня знаний ребёнка, закрепляя понятое и постепенно усложняя материал. Такой подход к отработке темы даёт устойчивый результат – видимый прогресс и полное усвоение темы. Если Вы ищете эффективный инструмент внеучебной подготовки школьника по математике и не только, приходите на iSmart.