Окружность и круг: такие похожие и такие разные. Узнаем почему
Окружность и круг: такие похожие и такие разные. Узнаем почему

Что такое круг и окружность? Может ли пустота превратить одну геометрическую фигуру в другую? В этой статье выясним это, а также расскажем о том, как называются части круга и окружности и как понять, где радиус, а где диаметр.
Определение круга и окружности
Окружность – это геометрическая фигура, замкнутая кривая, все точки которой равноудалены от центра.

Круг – это плоская геометрическая фигура, внутренняя плоскость, ограниченная окружностью. Кругом называется внутренняя часть окружности, которая включает и саму окружность.

Чтобы лучше понять разницу между окружностью и кругом, посмотрим на кольцо и тарелку.
Кольцо внутри пустое, у него есть только линия, которая ограничивает пустоту внутри. Именно так выглядит окружность. Внутри неё пустота.

Совсем другое дело тарелка. У неё есть линия, которая её ограничивает, но и внутри тарелка заполнена. Если бы она была пустой, из неё бы выпала еда. Тарелка – это круг, заполненная фигура.

Поэтому пустота действительно может превратить одну геометрическую фигуру в другую – круг в окружность.
Части окружности и круга
Мы узнали, что круг и окружность – это разные геометрические фигуры, но у них есть общие элементы (центр, диаметр, радиус и др.). Давайте разберёмся, что это за элементы, как они обозначаются и как их измерить.
Центр – это та самая точка, от которой равноудалены (то есть находятся на равном расстоянии от неё) все точки окружности.

С кругом всё не так однозначно. Круг внутри заполнен точками. А они находятся на разном удалении от центра.
Радиус – это отрезок, проведённый от центра окружности (или круга) до любой точки на окружности. В математике радиус обозначают латинской буквой R.
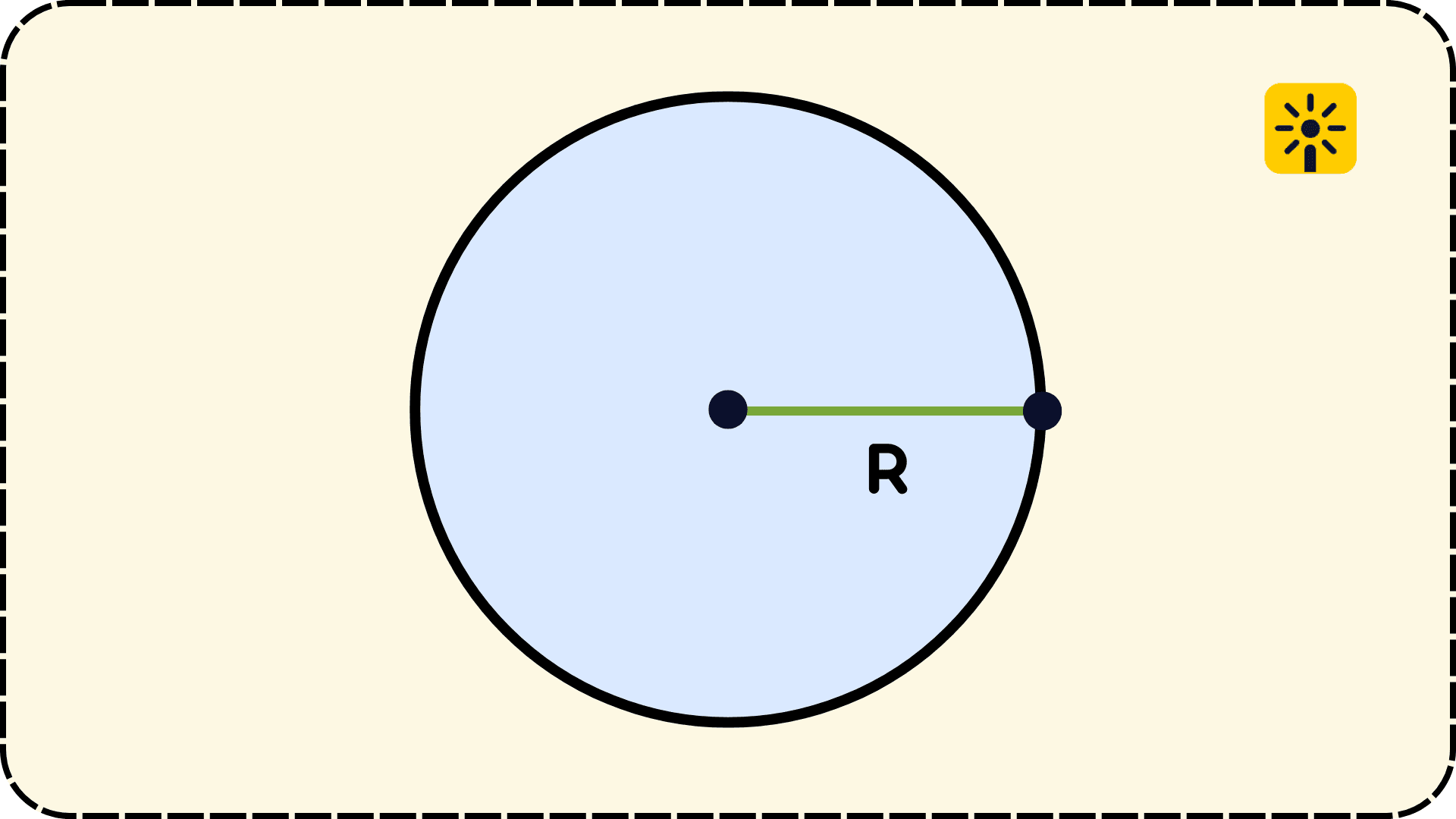
Чтобы измерить проведённый отрезок, можно взять линейку. Но если измерить нельзя, то находим радиус по формуле.
Существует несколько формул, с помощью которых можно найти радиус.
R = ½*D, где D — это диаметр нашей окружности. То есть радиус – это половина диаметра. Эту формулу школьники узнают в третьем классе.
Более сложной формулой, которую изучают в программе шестого класса школы, является вычисление радиуса с помощью длины окружности.
R = C/2 π, где C — длина окружности, а π — постоянная математическая величина, называемая числом Пи (приблизительно равно 3,14).
Ещё один элемент и окружности, и круга называется диаметр.
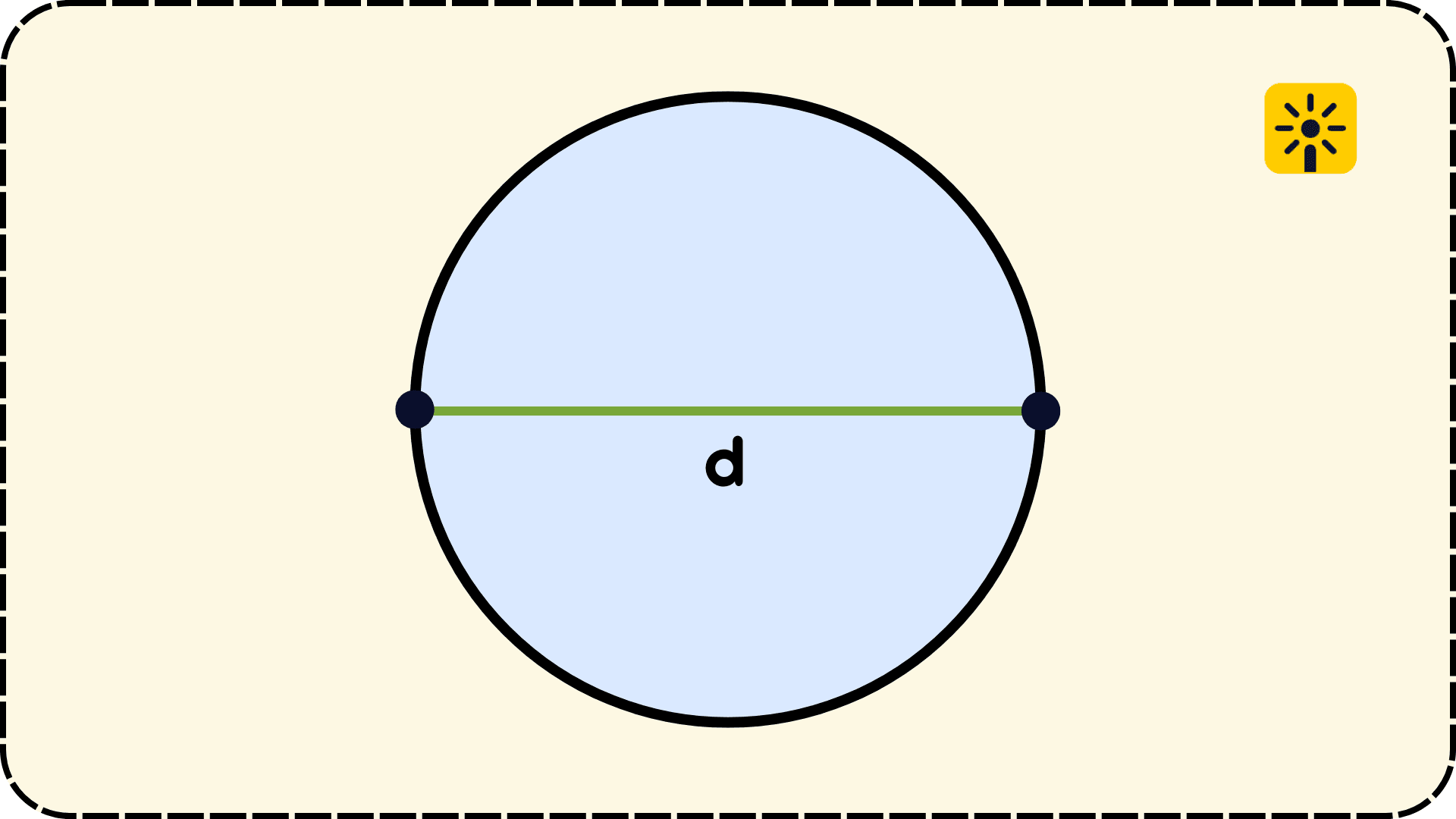
Диаметр – это отрезок, который проходит через центр окружности (или круга) и соединяет две точки на окружности. В математике диаметр обозначают латинской буквой D.
Диаметр состоит из двух радиусов, которые проведены по разные стороны от центра окружности. Диаметр также можно измерить линейкой, если он проведён через окружность (круг), или измерить по формуле.
В первом случае ищем диаметр через радиус окружности (круга). >D = 2R, где D — диаметр окружности, а R — её радиус.
Во втором случае ищем диаметр с помощью длины окружности (круга).
D = C/π, где D — диаметр окружности, C — её длина, а π — постоянная математическая величина, называемая числом Пи (приблизительно равно 3,14).
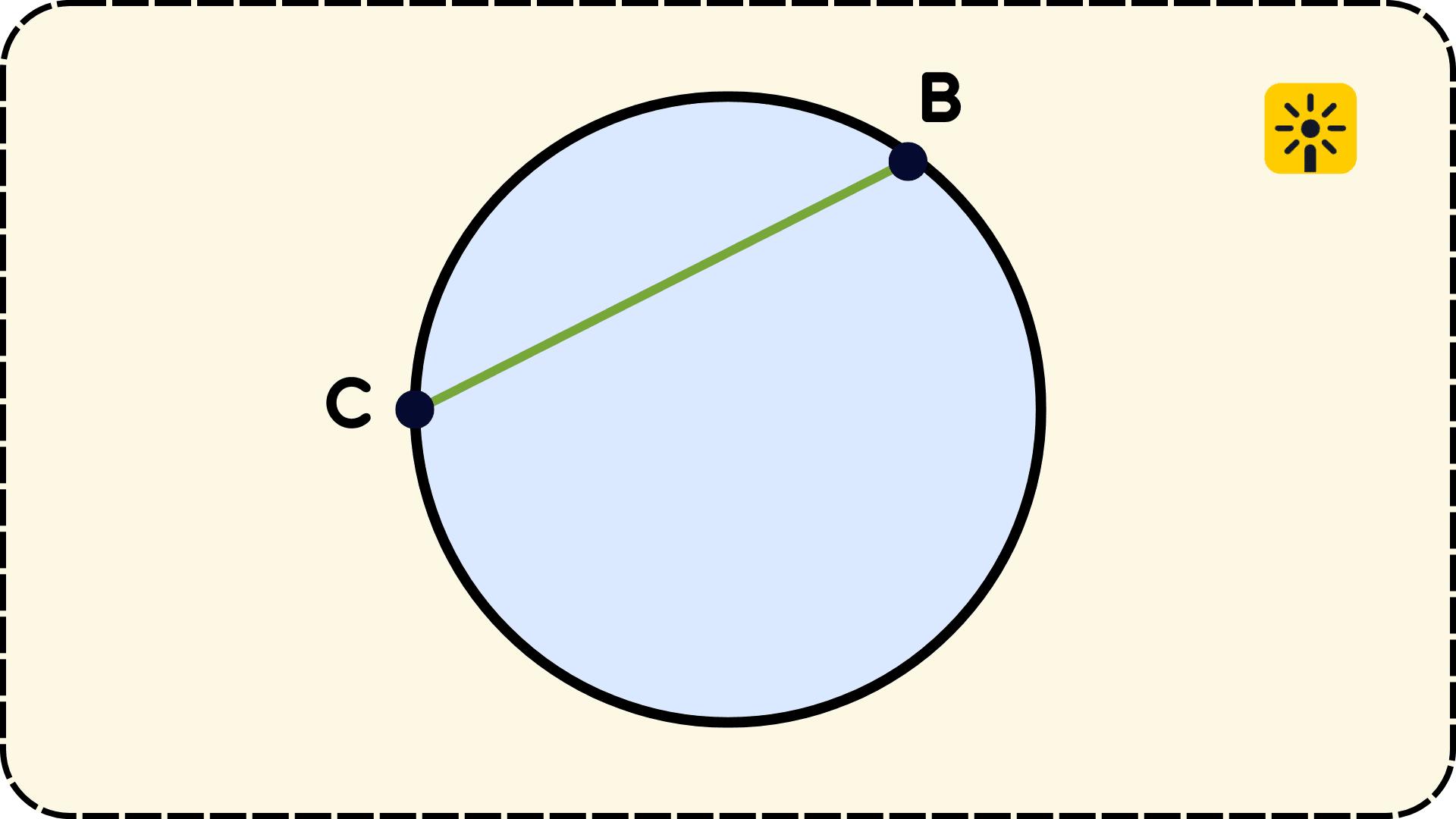
Хорда – отрезок, который соединяет две любые точки окружности. Хорду не обозначают отдельной буквой, а чаще всего называют по конечным точкам отрезка. Здесь хорда будет обозначаться СВ. Диаметр – это самая длинная хорда.
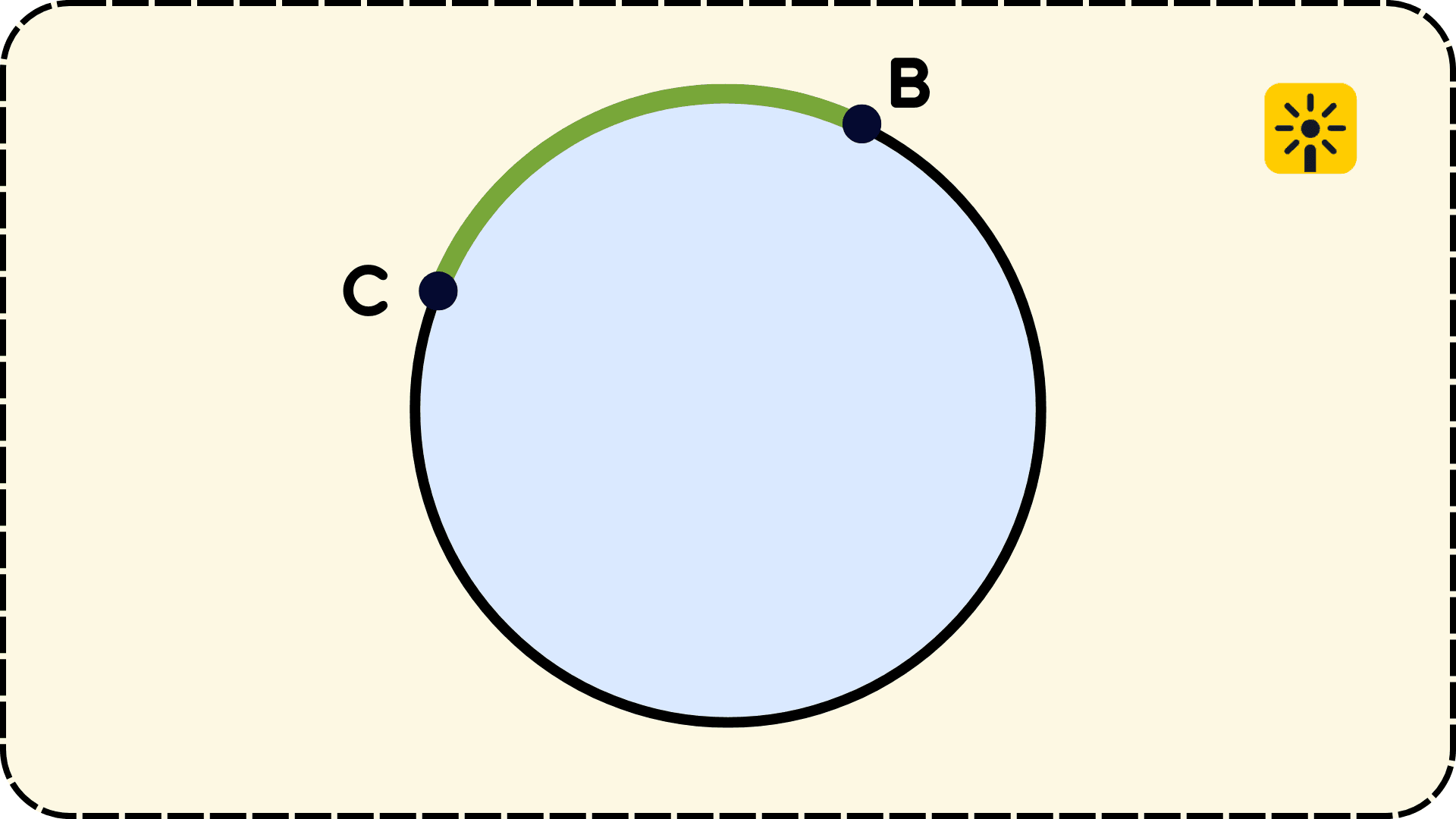
Дуга – это часть окружности, кривая, ограниченная двумя точками. На рисунке показаны две дуги. Одна выделена зелёным цветом, другая — голубым.
Части круга на примере торта
Есть части круга, которые нужно знать. И это пригодится не только в математике, но и в обычной жизни.
Сектор – это часть круга, которая ограничивается окружностью и двумя радиусами. По форме – треугольник с закруглённой стороной. Сектор ограничивают радиусы и дуга.

Если мы захотим отрезать только один кусочек торта, то и отрезанный кусочек, и оставшаяся часть торта будут секторами круга. Теперь разрежем торт по-другому. Отрежем кусочек по прямой, не проходя через середину торта. Так мы отрежем сегмент торта.

Сегмент – это часть круга, которая ограничивается окружностью и прямой линией, проведённой от одной точки окружности до другой (эта линия будет хордой). То есть сегмент ограничен хордой и дугой. Причем одна хорда является стороной для обоих сегментов: и отрезанный кусочек торта, и оставшаяся часть торта будут сегментами.
Хотите знать больше?
Геометрия часто бывает трудным предметом для школьников. Именно в этом разделе математики возникают первые проблемы, которые потом приводят к сложностям на ОГЭ и ЕГЭ.
Чтобы не допустить возникновения пробелов, лучше сразу отработать трудные темы на 100%. Именно такой формат предоставляет образовательная платформа iSmart. Система будет подбирать нужный материал и практические задания для ребёнка, исходя из его индивидуального уровня подготовки. И продолжит предлагать отработку навыка, пока статистика не покажет полное усвоение темы.
Задания, подготовленные профессиональными практикующими педагогами и психологами, заточены на применение наиболее эффективных и комфортных для ребёнка способов и методов подачи и восприятия материала.
Родителям останется только получать данные с рекомендациями о работе школьника на платформе в личный кабинет. Регистрируйтесь на iSmart и забудьте о временах, когда ребёнок не хотел заниматься сам.
Читайте также статьи:
Читать также





