Компоненты деления
Компоненты деления
Содержание:
Что такое деление
Деление — это один из ключевых математических процессов, который дети начинают изучать во втором классе. Понимание компонентов деления — делимого, делителя, частного и остатка — является важным шагом в изучении математики во втором классе.
Многие математические темы, изучаемые в старших классах, основываются на понятиях деления. Например, дроби, проценты и пропорции требуют глубокого понимания деления. Освоение компонентов деления во втором классе подготавливает детей к успешному изучению этих тем в будущем.
В этой статье мы рассмотрим основные компоненты деления и их значение.

Компоненты деления
Когда мы говорим о делении, важно понимать, что этот процесс включает несколько ключевых компонентов:
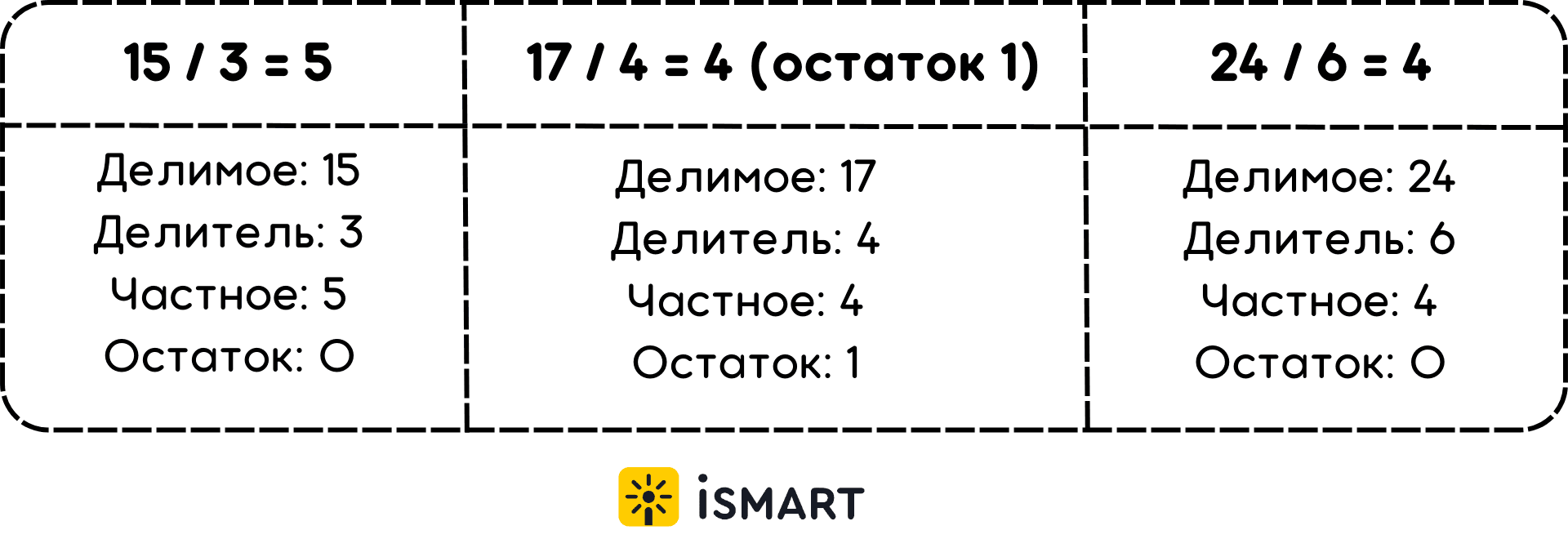
Делимое — это число, которое подлежит делению. Оно всегда стоит первым в записи деления. Например, в задаче 20 / 4 = 5, число 20 является делимым.
Делитель — это число, на которое делится делимое. Оно стоит вторым в записи деления. В примере 20 / 4 = 5, число 4 является делителем.
Частное — это результат деления делимого на делитель. В задаче 20 / 4 = 5, число 5 является частным.
Остаток — это то, что остается после деления, если делимое не делится нацело на делитель. Например, в выражении 13 / 3 = 4 (остаток 1), число 1 является остатком.
Рассмотрим несколько примеров, которые помогут ученикам второго класса лучше понять деление и его компоненты:
Деление помогает узнать количество частей в целом
Деление позволяет нам определить, сколько частей содержится в целом. Рассмотрим пример:
У нас есть 12 яблок, и мы хотим разделить их поровну между 4 детьми. Сколько яблок получит каждый ребенок? Чтобы найти ответ, мы делим 12 на 4: 12 / 4 = 3. Это означает, что каждый ребенок получит по 3 яблока. Чтобы найти ответ, мы делим 12 на 4: 12 / 4 = 3. Это означает, что каждый ребенок получит по 3 яблока.
В этом примере 12 — это делимое, 4 — делитель, а 3 — частное. Деление помогает нам понять, что если мы разделим 12 яблок на 4 части, каждая часть будет содержать 3 яблока.
Деление помогает узнать, чему равна часть, которая содержится в целом
Деление также позволяет нам определить, чему равна одна часть, которая содержится в целом. Рассмотрим другой пример:
У нас есть 15 конфет, и мы хотим узнать, сколько конфет приходится на каждого ребенка, если у нас 5 детей. Чтобы найти ответ, мы делим 15 на 5: 15 / 5 = 3. Это означает, что каждая часть (доля) содержит 3 конфеты.Чтобы найти ответ, мы делим 15 на 5: 15 / 5 = 3. Это означает, что каждая часть (доля) содержит 3 конфеты.
В этом примере 15 — это делимое, 5 — делитель, а 3 — частное. Деление помогает нам понять, что если мы разделим 15 конфет на 5 частей, каждая часть будет содержать 3 конфеты.
Связь между компонентами деления
Рассмотрим, как изменение делителя влияет на результат деления.
Если делимое остается неизменным, то при увеличении делителя значение частного уменьшается.
Например, если у нас есть 20 (делимое) и мы делим его на 4 (делитель), мы получаем частное 5 (20 / 4 = 5). Если мы увеличим делитель до 5, частное уменьшится до 4 (20 / 5 = 4).
Если делимое остается неизменным, то при уменьшении делителя значение частного увеличивается.
Например, если у нас есть 20 (делимое) и мы делим его на 5 (делитель), мы получаем частное 4 (20 / 5 = 4). Если мы уменьшим делитель до 4, частное увеличится до 5 (20 / 4 = 5).
Особые случаи деления
Деление числа самого на себя — это особый случай в математике, который всегда даёт один и тот же результат. Когда любое число делится само на себя, результатом всегда будет 1. Это связано с тем, что любое число содержится в самом себе ровно один раз.
Например:
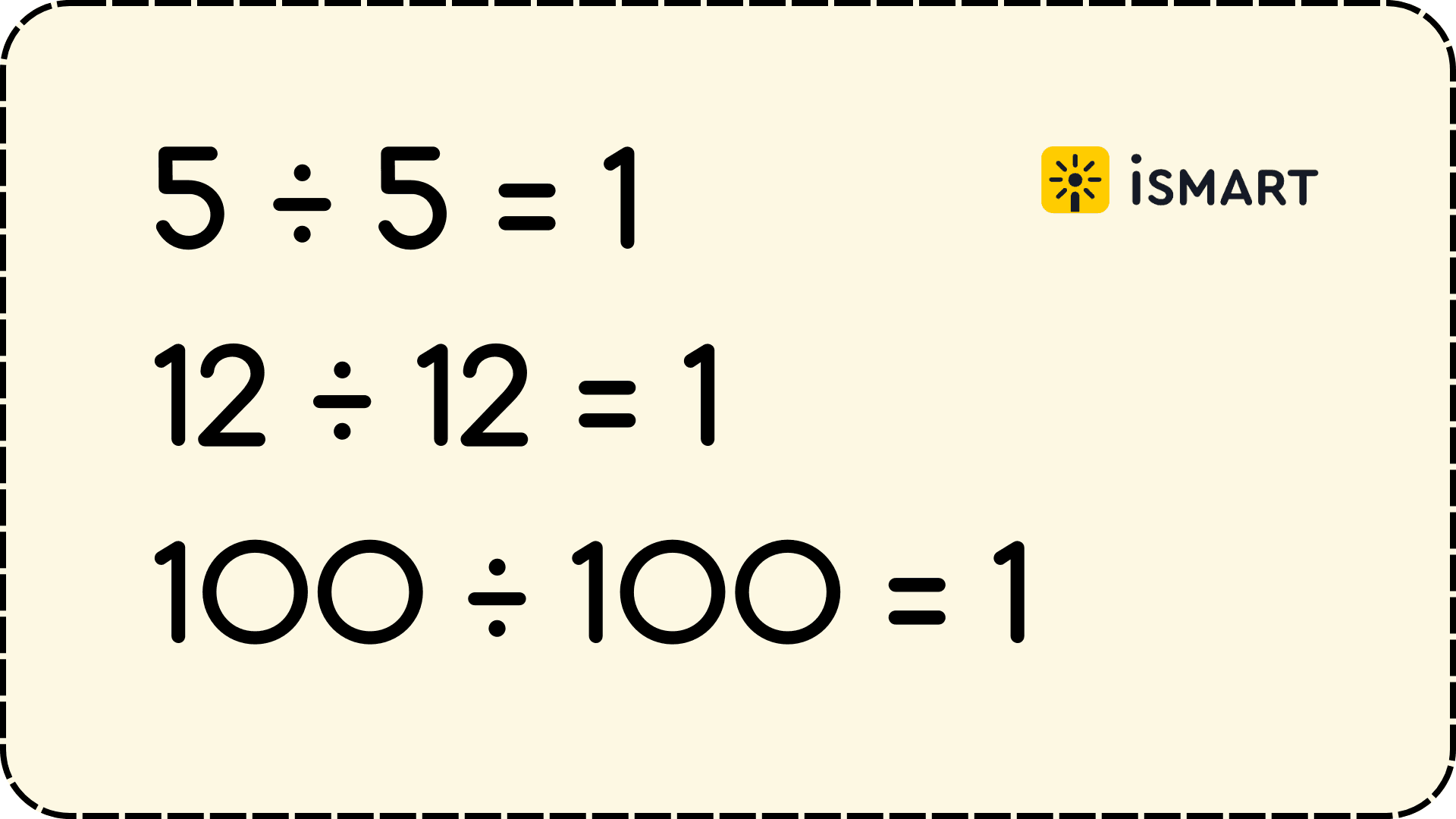
Объяснение:
Когда мы делим число само на себя, мы по сути спрашиваем, сколько раз это число помещается в самом себе. Ответ всегда будет один раз, независимо от того, какое число мы используем.
Деление числа на 1 — это один из самых простых случаев деления. Когда мы делим любое число на 1, результат всегда равен самому этому числу. Это связано с тем, что любое число делится на 1 ровно один раз. Таким образом, деление на 1 не изменяет значение делимого. Например:
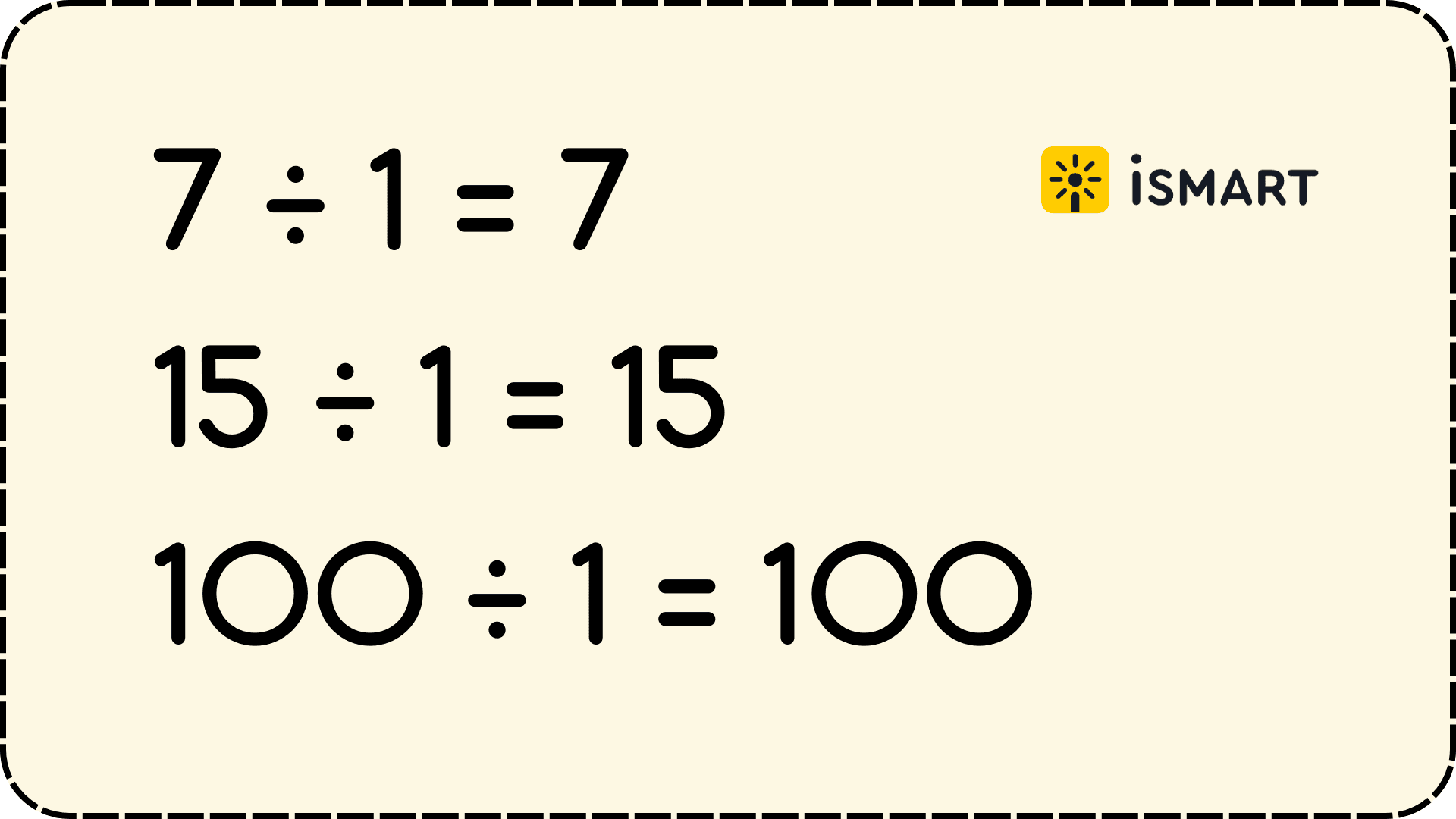
Деление 0 на любое число — когда 0 делится на любое ненулевое число, результатом всегда будет 0. Это связано с тем, что 0 не содержит в себе никаких частей, независимо от того, на сколько частей мы пытаемся его разделить. Например:
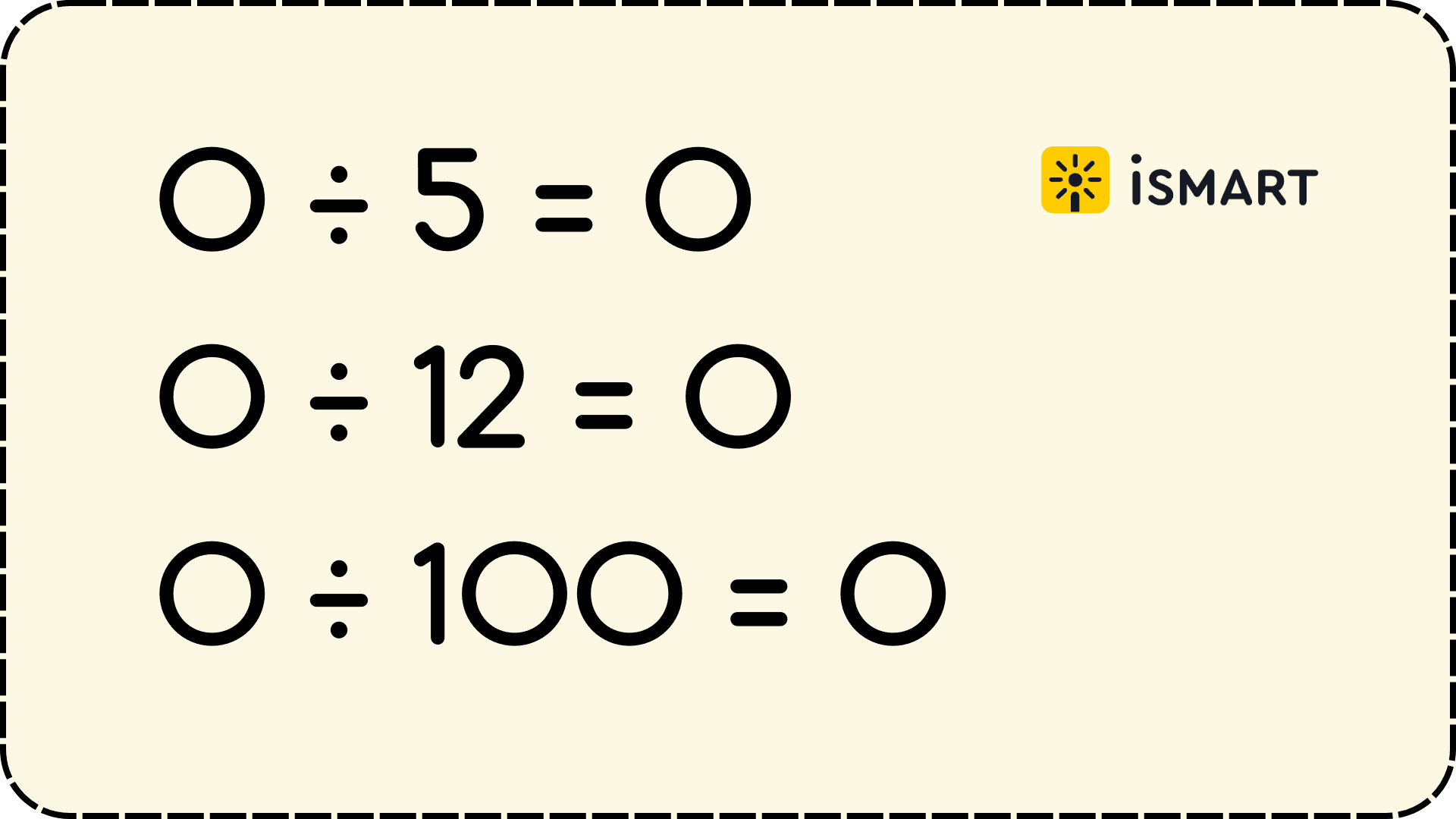
Объяснение:
Когда мы делим 0 на любое число, мы по сути спрашиваем, сколько раз 0 помещается в это число. Поскольку 0 не содержит никаких значимых частей, ответ всегда будет 0. Это правило помогает детям лучше понять основные принципы деления и его взаимосвязь с другими математическими операциями.
Деление на 0 — в математике деление на 0 невыполнимо, потому что оно не имеет смысла. Невозможно разделить какое-либо число на нуль, так как это противоречит основным принципам арифметики. Нужно просто запомнить, что на нуль делить нельзя!
Из статьи мы узнали
Что такое деление
Деление — это важная математическая операция, которая позволяет нам понять, сколько частей можно получить из целого и чему равна каждая часть. Эта операция противоположна умножению, поэтому мы можем использовать деление, чтобы найти один из множителей. Деление играет ключевую роль в математике и помогает решать множество практических задач в повседневной жизни.
Из каких компонентов состоит деление
Как компоненты деления взаимосвязаны
Если делимое остаётся неизменным, то при увеличении делителя значение частного уменьшается, а при уменьшении делителя значение частного увеличивается.
Если делитель остаётся неизменным, то при увеличении делимого значение частного увеличивается, а при уменьшении делимого значение частного уменьшается.
Особые случаи деления
Для более подробного изучения темы деления и его компонентов, вы можете воспользоваться образовательной платформой iSmart.org. В разделе «Математика за 2 класс» представлено множество примеров. Занимаясь всего по пятнадцать минут в день, ваш школьник добьётся отличных результатов. Регулярная практика поможет научиться решать примеры на деление быстро и эффективно. Переходите по ссылке iSmart.org и начинайте заниматься прямо сейчас!
Читать также