Представьте, что мы говорим о герое сказки. Положительный персонаж – это кто-то хороший, добрый, но если персонаж отрицательный – то он злой, плохой. А как обстоят дела с числами? У них тоже положительные хорошие, а отрицательные плохие? В статье разберёмся, как распознать положительные и отрицательные числа и как их складывать, вычитать, умножать и делить.

Кто у нас справа и слева от нуля?

Давайте посмотрим на рисунок. На нём линия со стрелкой, и стрелка показывает направление. Такую линию со стрелкой, поделённую на единичные (в нашем случае за единицу принят отрезок в 1 см) отрезки, ещё называют координатной прямой. Координатная прямая поделена на отрезки с подписанными внизу цифрами. Точка начала отсчёта – нуль.

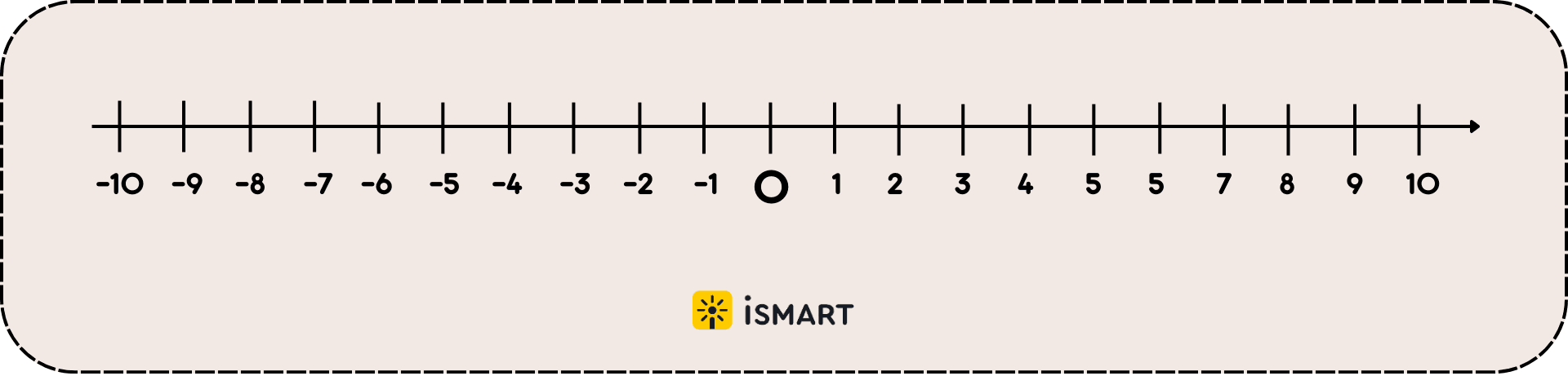
Справа от нуля цифры 1, 2, 3 и так далее. Перед ними никакого знака нет. А вот слева от нуля – цифры со знаком минус: -1, -2, -3. Именно такие числа называют отрицательными.

Отрицательные числа – это числа, которые меньше нуля, стоят слева от него на координатной прямой и на письме обозначаются знаком минус.

Положительные числа – это числа, которые больше нуля, стоят справа от него на координатной прямой и на письме знаком не обозначаются.

Это сделано для удобства, чтобы не писать знак плюс, ведь число со знаком + и без знака – это одно и то же число (5 и +5 одно и то же).

Исключение – случаи, когда мы говорим и пишем о температуре воздуха. Тут обязательно нужен знак. Если -20, надеваем тёплую куртку, шапку и варежки. Если +20, футболку и шорты.

Что такое модуль?

В школе для решения примеров с положительными и отрицательными числами используется понятие «модуль».

Модуль – это расстояние от начала отсчёта (от нуля) до точки координатной прямой, соответствующей этому числу.

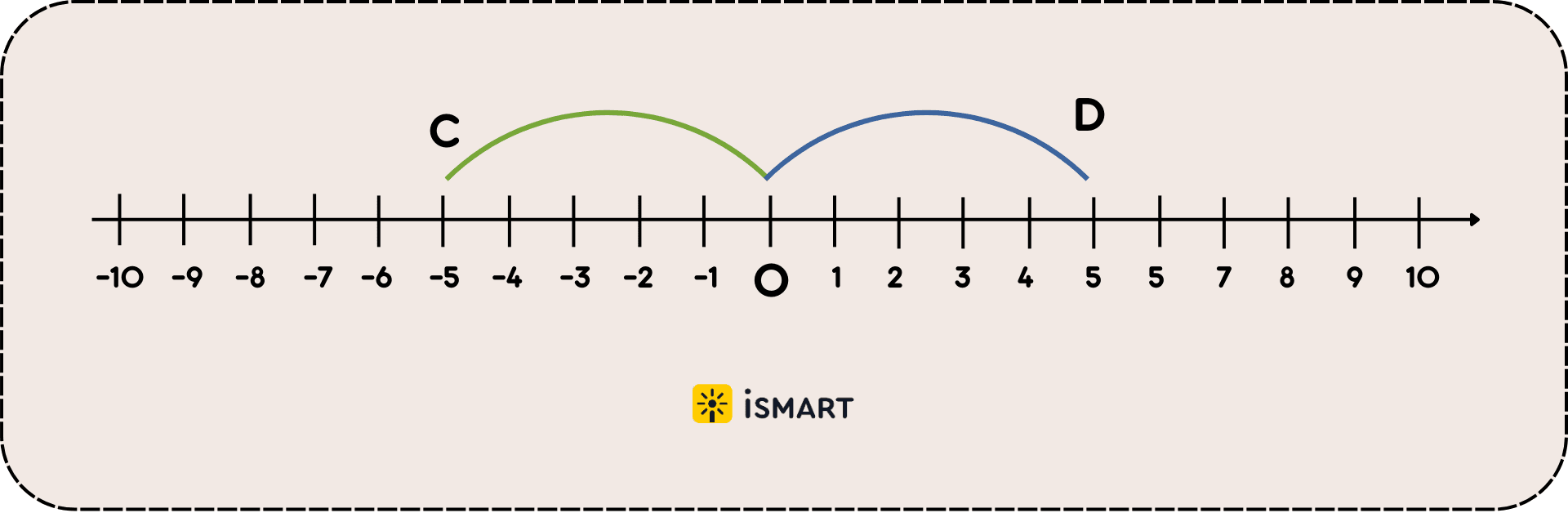
Расстояние от точки С (-5 на координатной прямой) до начала отсчёта (до нуля) равно пяти единичным отрезкам. Модуль записывается с помощью двух вертикальных линий слева и справа от числа. Значит, модуль числа -5 будет равен 5.

Расстояние от точки D (5 на координатной прямой) до начала отсчёта (до нуля) равно пяти единичным отрезкам. Значит, модуль числа 5 будет равен 5.

Следует запомнить важное правило. Положительное и отрицательное числа, которые отличаются только знаком, называются противоположными (например, 9 и -9).

Правила действий с положительными и отрицательными числами

Действия с положительными и отрицательными числами проходят в 6 классе. С такими числами можно совершать все арифметические действия: сложение, вычитание, умножение и деление. Но важно знать правила, иначе получишь неправильный ответ.

Сложение и вычитание с положительными и отрицательными числами

Если у нас и первое и второе число положительное и нам нужно их сложить, всегда получится положительное число.

Если у нас и первое и второе число отрицательное и нам нужно их сложить, всегда получится отрицательное число.

Причём, когда мы складываем два отрицательных числа, мы их пишем в скобках, а знак минус выносим за скобки. В скобках мы складываем не сами числа, а их модули. После того, как сложили модули чисел в скобках, к получившемуся числу в ответе ставим знак минус, который был за скобками.

Если одно число положительное, а второе отрицательное, очень важно понять, модуль какого из чисел больше.

Если больше модуль отрицательного числа, при сложении знак минус выносим за скобки, а в скобках вычитаем из модуля большего числа модуль меньшего. В ответе получится отрицательное число.

Если больше модуль положительного числа, при сложении знак плюс мысленно выносим за скобки, а в скобках вычитаем из модуля большего числа модуль меньшего. Можно поставить знак плюс для наглядности перед скобками, а можно не ставить. В ответе получится положительное число.

Если у нас и первое и второе число положительное и нам нужно их вычесть друг из друга, есть два типа примеров.

Тип 1 – первое число больше второго.

Здесь нет никаких подвохов и сложностей. В ответе получится положительное число.

Тип 2 – первое число меньше второго.

Здесь важно не смешивать знак числа и знак действия. Знак в таком примере меняется на противоположный и у арифметического действия, и у вычитаемого числа. Вычитание (минус) превращается в сложение (плюс), а положительное число 5, превращается в отрицательное (-5). В ответе получится отрицательное число.

Если у нас и первое и второе число отрицательное и нам нужно их вычесть друг из друга, запомним выражение: «Минус на минус даёт плюс». Оно как раз про этот случай. Ответ зависит от того, модуль какого числа больше.

В ответе получится положительное число.

В ответе получится отрицательное число.

Если одно число положительное, а второе отрицательное, знак вычитаемого меняется на противоположный, а вычитание превращается в сложение, так как тут тоже действует правило «минус на минус дает плюс». Знак ответа, как и при сложении, зависит от того, модуль какого числа больше – положительного или отрицательного.

В ответе получится положительное число.

Умножение и деление с положительными и отрицательными числами

Если мы умножаем два положительных числа, то в ответе получим положительное число.

Если мы умножаем два отрицательных числа, то в ответе получим положительное число. Применяем правило «минус на минус дает плюс».

Если одно число положительное, а второе отрицательное, то при умножении в ответе будет отрицательное число (со знаком минус).

Такое же правило действует и при делении. Если оба числа положительные или оба числа отрицательные, в ответе получаем положительное число.

Если одно число положительное, а второе отрицательное, то при делении в ответе будет отрицательное число (со знаком минус).

Для наглядности представим правила действий с отрицательными и положительными числами в таблице.

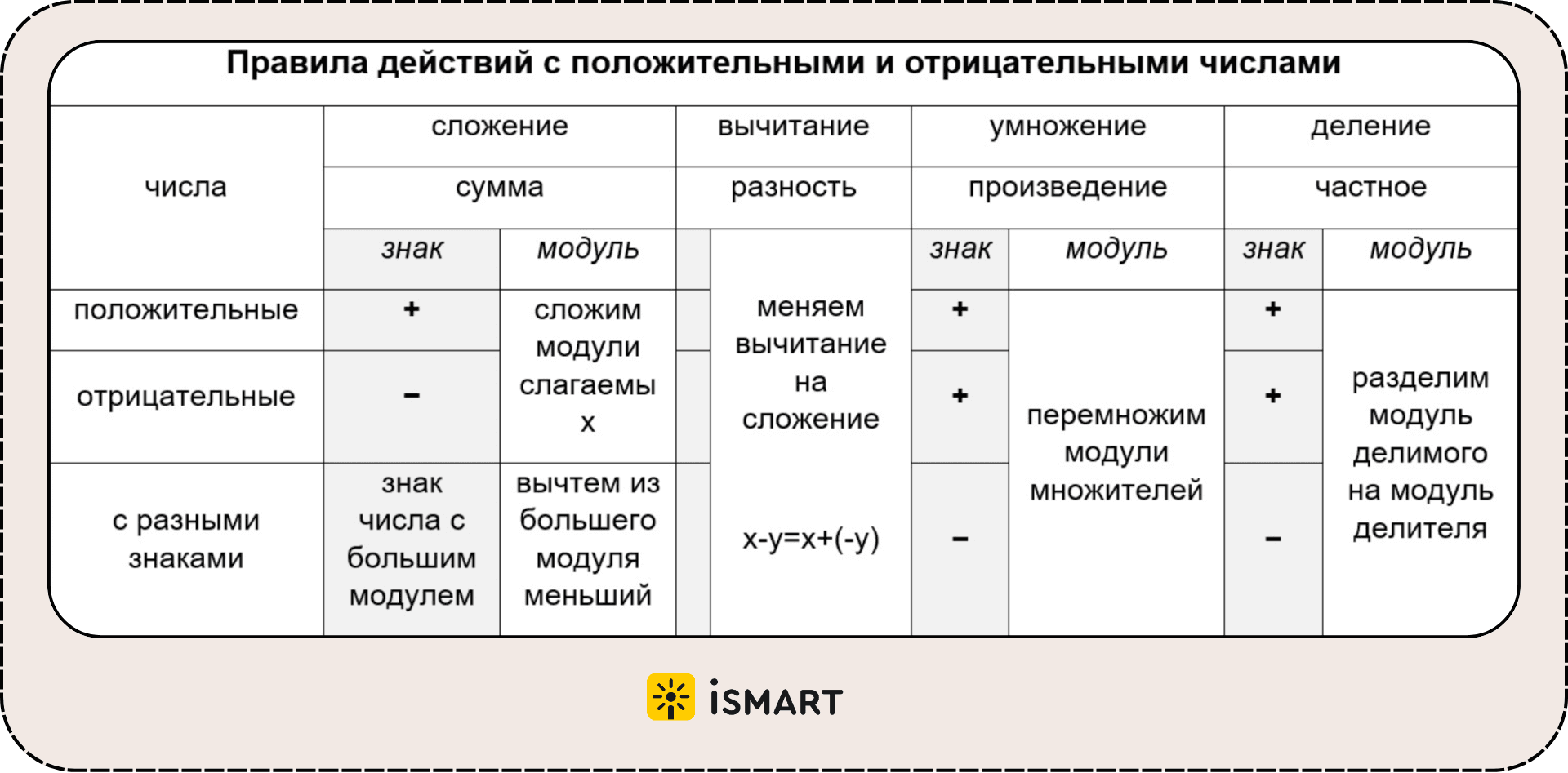
Правила действий с положительными и отрицательными числами подходят как для натуральных чисел, так и для дробей.

Учеба со знаком плюс

В математике положительные и отрицательные числа – это не плохие и хорошие, а просто те числа, которые нужно знать. И знать, как правильно решать примеры с ними. Чтобы у ребёнка не было проблем в школе, нужно как можно больше практиковаться в решении примеров на трудную тему. Но как этого добиться, если тема не даётся, тяжело сделать даже домашнее задание, а Вам нужно ещё и дополнительно позаниматься?

Решение проблемы – использование онлайн-платформ. На образовательной платформе iSmart более 300 000 заданий по разным предметам школьной программы. Понятно, что ни один учебник не предложит такого количества упражнений на отработку проблемной темы. К тому же задания на платформе разноплановые, увлекательные и не дадут ребёнку заскучать и быстро утомиться.

Конечно, потрудиться придётся. Целых 15–20 минут в день нужно потратить на выполнение блока заданий iSmart по выбранной теме. Но и результат впечатляет – четвёрки и пятёрки в дневнике и ребёнок, который научится не только решать трудные примеры, а ещё и заниматься самостоятельно и с интересом. Регистрируйтесь на iSmart, чтобы испытывать от учёбы только положительные эмоции.