Учителя жалуются, что текстовые задачи на уроках по математике традиционно вызывают у школьников проблемы. Говорят, что дети не хотят рассуждать, ленятся. Но только ли в этом дело? Или ребёнку просто трудно бывает разложить задачу на нужные составляющие, чтобы спокойно справляться с заданием? И часто не хватает практики по отработке темы. В этой статье разберёмся, зачем нужны текстовые задачи, какими они бывают, как их решать. А также дадим памятку, как рассуждать при решении текстовых задач, чтобы ребёнку было проще.

Палочка-выручалочка для тренировки мышления

Изначально обучение математике велось через решение практических задач, где были описаны ситуации, которые могли пригодиться, например, в торговле. Ученик просто повторял действия за учителем, должен был заучивать решение. В дальнейшем педагоги поняли, что решение текстовых задач помогает тренировать логическое и практическое мышление, способствует развитию речи, учит чётко формулировать ситуацию.

Текстовая задача помогает перевести ситуации из нашей обычной жизни на математический язык – в математические символы и знаки. Именно успехи в развитии способности к самостоятельному мышлению и практическая полезность делают текстовые задачи такими важными в процессе обучения школьников.

Но многие дети не любят решать задачи, так как пугаются процентов, дробей и других математических величин. Чтобы убрать эти страхи, ребёнку нужно понять ситуацию, описанную в задаче, представить себе, что, например, дробь – это просто часть целого, как кусочек – часть большого торта. Давайте попробуем разложить все сложности решения текстовых задач на такие простые этапы, чтобы школьнику тема показалась лёгкой, как дважды два – четыре.

Как понять текстовую задачу?

Любая текстовая задача состоит из двух частей – условия и вопроса (требования). В условии сообщаются известные сведения о людях или предметах, о которых говориться в задаче. Даются числовые данные, чтобы мы могли решить задачу. В вопросе нас просят найти неизвестное.

Например, задача:

Найдите скорость моторной лодки по течению реки – это вопрос (требование).

Работая над любой задачей, нужно сначала прочитать её, лучше вслух, чтобы легче было понять и представить, о чём говорится в задаче. Потом выбираем из условия задачи то, что нам известно. Записываем известное в виде краткой записи. Записываем кратко то, что нужно узнать. Понимаем, какой это тип задачи. Если знаем, как решаются задачи такого типа, решить задачу будет несложно.

Производим вычисления на черновике и получаем ответ. Подставляем ответ и проверяем решение. Если всё сходится, значит решение верное и его можно записать в чистовую тетрадь.

Методы решения текстовых задач

В 6 классе чаще всего встречаются арифметический метод или сочетание логического метода с арифметическим.

Арифметический метод. Если решаем задачу арифметическим методом – ищем ответ на вопрос задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами.

Логический метод. Решить задачу логическим методом – значит найти ответ на вопрос задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.

Типы задач и способы их решения

Решение задач на нахождение части от целого и целого по его части

Задача

Решение:

Так как Маша выиграла 1/3 конфет, то она выиграла одну из трёх частей конфет, то есть у неё в 3 раза меньше конфет, чем было разыграно. Так как Маша выиграла 8 конфет, что составляет 1/3 от общего числа, у неё одна из трёх частей общего количества конфет. Общее количество конфет можно найти, умножив одну часть на три. Значит общее число конфет: 8⋅3=24

Ответ: 24.

Логические задачи

Задача

Решение:

Найдём количество бананов, которое съедают 10 обезьянок за 1 день. 100/5=20 бананов — съедают 10 обезьянок за 1 день. Далее найдём, сколько за 1 день съедает одна обезьянка, поделив количество съеденных десятью обезьянками бананов на количество обезьянок. 20/10=2 банана — съедает одна обезьянка за 1 день.

Чтобы найти, сколько съедают 7 обезьянок за 1 день, нужно умножить полученное значение на количество обезьянок. 7⋅2=14 бананов — съедят 7 обезьянок за 1 день.

А чтобы найти, сколько за 7 дней съели бананов 7 обезьянок, нужно умножить 14 на количество дней. 14⋅7=98 бананов.

Ответ: 98 бананов.

Решение задач арифметическим способом

Задача

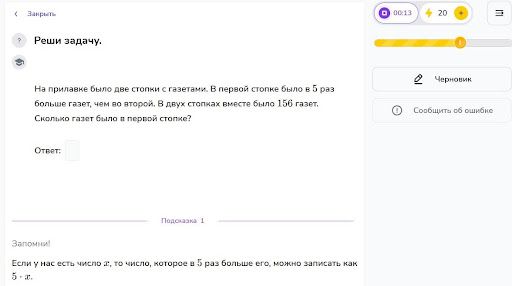
Решение

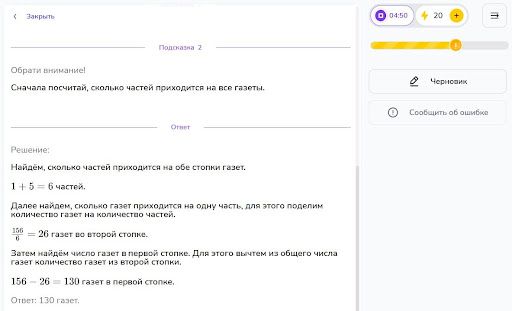
Решение задач перебором всех возможных вариантов

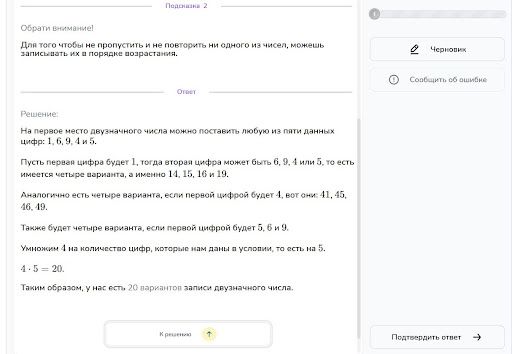
Задача

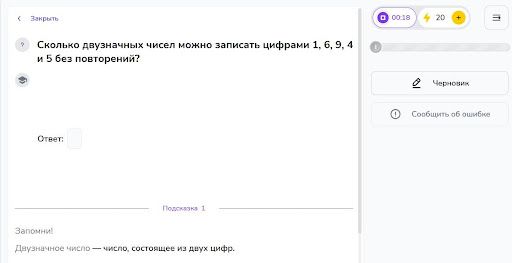
Решение:

Решение задач на зависимость величин время-скорость-расстояние

Задача

Решение:

Найдём скорость расхождения кораблей: для этого сложим их скорости. 72+59=131 км/ч — общая скорость кораблей.

Для того, чтобы найти расстояние между кораблями через 6 часов, нужно умножить их общую скорость на время.

131⋅6=786 км — расстояние будет между кораблями через 6 часов.

Ответ: 786 км.

Решение задач на зависимость величин цена-количество-стоимость

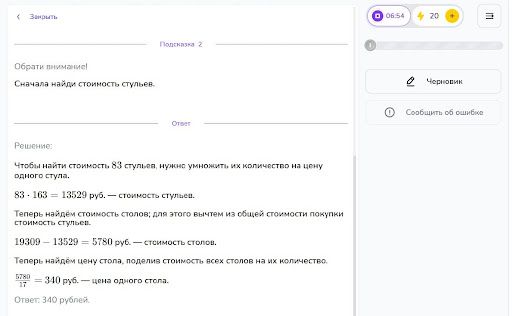
Задача

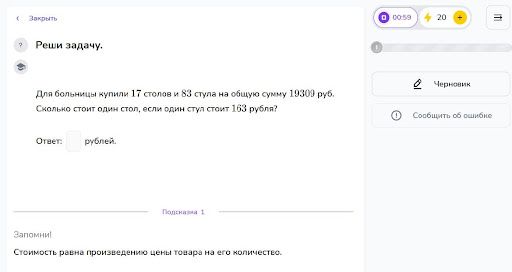
Решение:

Решение задач на зависимость величин производительность-время-объём работы

Задача

Решение:

Чтобы найти производительность второго работника, нужно производительность первого работника поделить на 3. 21,75/3=7,25 деталей в час — производительность второго работника.

Затем найдём общую производительность. Для этого сложим производительности рабочих. 21,75+7,25=29 деталей в час — общая производительность двух работников.

Чтобы найти время, за которое работники выполнят задание, надо объем работы поделить на их общую производительность. 232/29=8 часов

Ответ: 8 часов.

Задачи на отношение, пропорциональность величин, проценты

Задача

Решение:

Согласно условию задачи, за день бабушка продала 15 кг яблок, что составляет 20% от первоначального их количества. Вычислим, сколько яблок было у бабушки первоначально.

Так как изначальное количество яблок представляет собой 100%, то составим отношение. 15 кг яблок относится к 20%, как изначальное количество яблок к 100%.

Обозначим через x изначальное количество яблок и составим пропорцию. 15/20=x/100

Чтобы найти неизвестный средний член пропорции, нужно произведение её крайних членов разделить на известный средний член пропорции. x=15⋅100/20

Найдём x: x=1500/20 х=75 кг яблок было у бабушки первоначально

Ответ: 75 кг.

Памятка «Как решать текстовые задачи»

Прочитай задачу и представь себе то, о чём в ней говорится.

•
Выдели условие и вопрос.
•
Запиши условие кратко.
•
Подумай, можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что надо узнать сначала, что потом?
•
Составь план решения.
•
Выполни решение.
•
Проверь решение и запиши ответ задачи.

Задачи на самопроверку

Задача №1

Если решение верное, в ответе должно получится 12 кг.

Задача №2

Если решение верное, в ответе должно получится 2000 м.

Решаем текстовые задачи легко

Если вы попробовали решить текстовые задачи и это не совсем получилось, не огорчайтесь. Есть способ натренировать навык решения таких задач. Достаточно зайти на платформу iSmart в раздел «Математика», выбрать 6 класс, пункт «Решение текстовых задач», и там вы найдёте разные типы задач для отработки. Ребёнок решает задачи сам. Если не справился, система подскажет, как лучше решать подобные задачи, даст правильной ход рассуждений. 15–20 минут в день – и задачи будут решаться на раз-два-три.